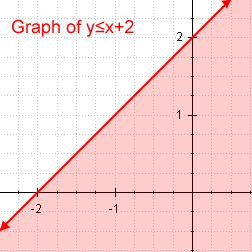
Another Look at Linear Equations: Algebra Chapter 2 Section 4
Hello internet, and welcome to the Algebra Lecture Series from The Science of Life. This entry is an introduction to Linear Functions in both graphs and models. There are two situations where the slope would not be stated in the slope-intercept form. These are cases where the line crosses only one of the 2 (or more) axes. First, let's consider the horizontal line. If we have a line which has a y-intercept but does not have an x-intercept (does not cross the x-axis), it is called a horizontal line. Let's look at it from the point of view of the slope-intercept form we developed last time, $y=mx+b$. We know that the slope is the change in the y-value per change in the x-value. If we have two points $(x_{1}, y_{1})$ and $(x_{2}, y_{2})$, the slope is mathematically defined as $m=\frac{y2-y1}{x2-x1}$. The denominator, the $ dx=x2-x1$, is never going to be zero when there's a y-intercept, since we can go from the left of the y-intercept to th...